Archives de catégorie : javascript

Marching cubes sandbox

Laisser un commentaire

Nous avons mis en ligne une nouvelle démo : marching cubes sandbox que vous pouvez voir ici : http://www.spacegoo.com/marchingCubes
Pour les gens qui ne sont pas compatibles, nous avons réalisé une vidéo capture d’écran :

Marching Cubes Sandbox
Runtime
0:59
Compteur de vues
1,269

Dans cette démo, nous avons implémenté l’algorithme marching cubes dans un version modifiée. En effet, webgl ne permet pas d’accéder au geometry shader comme dans le code original. Nous avons donc du migrer la génération des vertex du côté du javascript, avant d’en faire le rendu par WebGL.

Rappelons brièvement comment fonctionne l’algorithme. Il s’agit de générer une géométrie à partir d’une fonction appelée « fonction de densité ». Celle-ci prend la forme f(x, y, z) = 0 Par exemple, si on veut générer une sphère, on prendra f(x, y, z) = x^2 + y^2 + z^2 - R^2

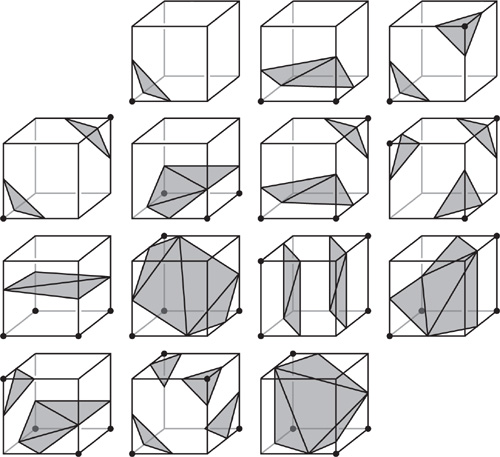
On divise ensuite l’espace en cubes ou « chunks » pour récupérer la terminologie initiale. Ceux-ci sont disposés dans l’ordre idoine (celui des z-croissants) au sein du cône de vue WebGL. Chacun d’entre eux est ensuite divisé en une grille de 32*32*32 « voxels » pour lesquels on va générer les vertex. Pour décider si l’on en génére ou non, on regarde les valeurs de la fonction au huit sommets du « voxel ». Si cette valeur est positive, on attribue la valeur 1 au sommet, sinon la valeur 0. On se retrouve avec 256 cas possibles, qui se réduisent à 14 modulo le groupe de symétrie du cube. Voici ces cas (l’image est tirée du site nVidia) :

Les 14 cas primitifs


Une fois qu’on a parcouru tous les voxels, on se retrouve donc avec un tableau contenant les sommets et les faces à générer.
Il y a alors deux problèmes.

  • La plupart des calculs qu’on effectue aboutissent à un voxel qui ne génère pas de vertex, soit qu’il soit complètement en dehors de la surface, soit qu’il soit complètement en dedans.
  • Une fois qu’on a généré la géométrie, la plupart des vertex sont générés en plusieurs exemplaires, ce qui alourdit le rendu. De plus, les vertex index buffers de webgl sont limités à 65536 sommets, puisqu’ils sont encodés sur des short.

    • Pour résoudre ces problèmes, nous avons choisi en première approche une solution qui n’est pas optimale, mais permet d’aboutir simplement à de bons résultats.
    Nous avons rêglé le premier problème en remplaçant chaque chunk par un octree dont la racine est le chunk en question et dont on subdivise les cellules seulement si elles doivent générer des vertex. Par une astuce, on peut aussi s’assurer que la fonction de densité ne sera jamais évaluée deux fois au même endroit.
    Le deuxième problème est beaucoup plus complexe, et nous avons choisi de générer les vertex doubles, mais de faire une passe de calcul supplémentaire où on les enlève. Nous faisons ceci par un tri rapide simultané sur les deux buffers (vertex et index) et puis en supprimant les doublons.

    Cette solution a l’avantage d’être rapide car le tri rapide ne prend que peu de temps. L’inconvénient est qu’au cours du calcul, juste avant la phase de tri, les buffers sont énorme (plus de 4 fois plus gros que nécessaire) ce qui surcharge de travail le garbage collector javacript et peut rapidement saturer la mémoire du navigateur. Il faut noter en passant que notre première implémentation de l’octree était récursive ce qui, quand ça ne faisant pas planter la call stack de javascript, explosait le garbage collector. Nous avons donc préféré l’implémenter à la main.
    Nous avons donc pour projet d’optimiser cela en reprenant l’idée originale de l’algorithme, qui consiste à « marcher » dans l’octree en suivant les composantes connexes de la surface à mailler.
    Mais cela fera l’objet d’un autre article plus détaillé!

    Pavages de Penrose

    Laisser un commentaire

    Pour notre future démo, nous nous sommes intéressés aux pavages de Penrose.
    Il s’agit de pavages non-périodiques du plan construits à partir de règles locales. Ainsi, contrairement aux pavages classiques périodiques qu’on peut voir par exemple dans les mosaïques de l’Alhambra, ceux-ci ne possèdent aucune règle qui permet de déduire l’ensemble du dessin par une suite finie de rotations/translations.
    En résultent des motifs surprenants et très beaux.
    D’un point de vue scientifique, ils servent à étudier les quasi-cristaux, notamment pour déterminer leurs figures de diffraction. Alain connes s’en sert également comme d’un exemple privilégié pour illustrer sa géométrie non-commutative.

    Nous allons décrire un algorithme pour construire de tels pavages à partir de triangles d’or. Un triangle d’or est un triangle isocèle dont le grand côté est \varphi fois plus long que le petit côté. Il n’en existe que deux types :
    On définit alors une procédure de découpage de ces triangles. Partant de l’un ou l’autre cas, on le coupe en deux suivant la méthode suivante :

    • A gauche : \lVert SR\rVert = \lVert RQ \rVert ou de manière équivalente : S = (2-\varphi)*P + (\varphi - 1)*Q
    • A droite : \lVert RP\rVert = \lVert RS \rVert   ou de manière équivalente : S = (\varphi - 1)*Q + (2-\varphi)*R

    Les triangles générés par un tel découpage sont également des triangles d’or, ce qui permet de réiterer la procédure. Il faut noter qu’à chaque subdivision, on a le choix entre une division « à gauche » ou « à droite », ce qui permet de générer autant de façon de paver le plan que nécéssaire.
    Nous avons fait le choix d’une méthode particulière, qui génère de beaux pavages, et en voici l’algorithme, en pseudo-code de type javascript, avec une gestion manuelle de la pile de récursion, pour éviter de la faire exploser à l’éxécution :

    // lvl donne le nombre de subdivisions
    penrose = function(lvl) {
    var Q = [100, 100];
    var R = [100, 500];
    var P = [716, 300];
    // lvl désigne la distance qui sépare le triangle de la subdivision maximale autorisée
    var root = Triangle(P, Q, R, "aigu", lvl);
    var stack = [];

    stack.push(root);
    // Tant que la pile de triangle non-subdivisés est non-vide :
    while (stack.length > 0) {
    var zde = stack.pop ();
    if (zde.prof <= 1) { // cas terminal
    zde.draw ();
    }
    else {
    // split renvoie le point S suivant la procédure décrite plus haut
    var S = zde.split ();
    if (zde.style === "aigu") {
    stack.push(Triangle(zde.R, S, zde.Q, "aigu", zde.prof-2));
    stack.push(Triangle(S, zde.P, zde.R, "obtus", zde.prof-1));
    }
    else {
    stack.push(Triangle(zde.R, zde.P, S, "aigu", zde.prof-1));
    stack.push(Triangle(S, zde.P, zde.Q, "obtus", zde.prof-2));
    }
    }
    }
    }

    Ce code termine puisqu’à chaque étape, on ne génère que des triangles dont la profondeur est strictement inférieure au triangle courant et que le cas terminal ne renvoie rien.

    Nous l’avons utilisé en javascript en dessinant un tel triangle découpé avec 16 niveaux de profondeurs :

    La démo est disponible ici :http://www.spacegoo.com/penrose

    Héritage en Javascript

    Le javascript est aujourd’hui largement utilisé sur le Web. Tous les navigateurs implémentent leur moteur javascript, et il est évidemment le langage incontournable quand il s’agit d’utiliser WebGL ou WebCL.

    Il est présenté comme un langage objet, mais ses capacités à ce niveau restent nativement limitées. Notamment, l’héritage n’est pas prévu. Lorsqu’on développe une application conséquente, l’héritage est pourtant un facteur indispensable pour réduire la quantité de code et donc les coûts de développement d’une application.

    Il existe plusieurs méthodes pour contourner cette faiblesse du langage, et nous allons vous en présenter une, qui est à notre avis la plus souple et la plus élégante. Selon la terminologie de Douglas Crockford, il s’agit d’un pattern d’héritage « fonctionnel ». Rien ne vaut un exemple, alors en voici un :


    var motherClass = function (spec) {
    var that = {}; // création de l'objet retourné
    that.get_name = function () { // "virtual" method
    }
    return that;
    }

    var daughterClass = function (spec) {
    spec.name = spec.name || "";
    var that = motherClass(spec); // l'héritage est ici : on initialise l'objet retourné en utilisant le constructeur de la classe mère
    that.get_name = function () { // on spécifie le code de la méthode "virtuelle" mère
    return "daughterClass : " + spec.name;
    }
    return that;
    }

    var instance = daughterClass({name: "daughter"}); // instanciation
    console.log(instance.get_name ()); 

    daughterClass : daughter

    On peut alors spécifier plusieurs classes héritant de « motherClass ».
    Une autre classe pourrait par exemple être :

    var daughterClass2 = function (spec) {
    spec.name = spec.name || "";
    var that = motherClass(spec); //héritage ici!
    that.get_name = function () { // et respecification de l'interface
    return "daughterClass2 : " + spec.name;
    }
    that.special_to_this_class = function () { // methode specifique à la classe daughterClass2
    return "special";
    }
    return that;
    }

    Et on peut alors utiliser cela dans un même tableau (c’est un avantage du non-typage javascript) :


    var tab = [];
    tab[0] = daughterClass({name: "1"});
    tab[1] = daughterClass2({name: "2"});

    for (var i = 0 ; i < 2 ; ++i) { console.log(tab[i].get_name ()); } 

    daughterClass : 1
daughterClass2: 2

    Après cela il ne tient qu’à vous d’enrichir les méthodes pour obtenir ce que vous voulez!

    PS : notez que dans ces classes, on ne peut accéder aux attributs autrement qu’avec la méthode get. C’est un forme d’encapsulation des données!