Pour notre future démo, nous nous sommes intéressés aux pavages de Penrose.
Il s’agit de pavages non-périodiques du plan construits à partir de règles locales. Ainsi, contrairement aux pavages classiques périodiques qu’on peut voir par exemple dans les mosaïques de l’Alhambra, ceux-ci ne possèdent aucune règle qui permet de déduire l’ensemble du dessin par une suite finie de rotations/translations.
En résultent des motifs surprenants et très beaux.
D’un point de vue scientifique, ils servent à étudier les quasi-cristaux, notamment pour déterminer leurs figures de diffraction. Alain connes s’en sert également comme d’un exemple privilégié pour illustrer sa géométrie non-commutative.
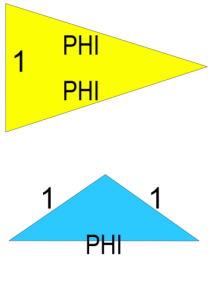
Nous allons décrire un algorithme pour construire de tels pavages à partir de triangles d’or. Un triangle d’or est un triangle isocèle dont le grand côté est 
On définit alors une procédure de découpage de ces triangles. Partant de l’un ou l’autre cas, on le coupe en deux suivant la méthode suivante :
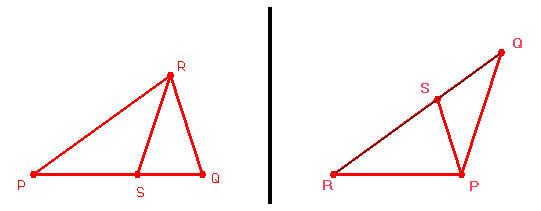
- A gauche :
ou de manière équivalente :
- A droite :
ou de manière équivalente :
Les triangles générés par un tel découpage sont également des triangles d’or, ce qui permet de réiterer la procédure. Il faut noter qu’à chaque subdivision, on a le choix entre une division « à gauche » ou « à droite », ce qui permet de générer autant de façon de paver le plan que nécéssaire.
Nous avons fait le choix d’une méthode particulière, qui génère de beaux pavages, et en voici l’algorithme, en pseudo-code de type javascript, avec une gestion manuelle de la pile de récursion, pour éviter de la faire exploser à l’éxécution :
// lvl donne le nombre de subdivisions
penrose = function(lvl) {
var Q = [100, 100];
var R = [100, 500];
var P = [716, 300];
// lvl désigne la distance qui sépare le triangle de la subdivision maximale autorisée
var root = Triangle(P, Q, R, "aigu", lvl);
var stack = [];
stack.push(root);
// Tant que la pile de triangle non-subdivisés est non-vide :
while (stack.length > 0) {
var zde = stack.pop ();
if (zde.prof <= 1) { // cas terminal
zde.draw ();
}
else {
// split renvoie le point S suivant la procédure décrite plus haut
var S = zde.split ();
if (zde.style === "aigu") {
stack.push(Triangle(zde.R, S, zde.Q, "aigu", zde.prof-2));
stack.push(Triangle(S, zde.P, zde.R, "obtus", zde.prof-1));
}
else {
stack.push(Triangle(zde.R, zde.P, S, "aigu", zde.prof-1));
stack.push(Triangle(S, zde.P, zde.Q, "obtus", zde.prof-2));
}
}
}
}
Ce code termine puisqu’à chaque étape, on ne génère que des triangles dont la profondeur est strictement inférieure au triangle courant et que le cas terminal ne renvoie rien.
Nous l’avons utilisé en javascript en dessinant un tel triangle découpé avec 16 niveaux de profondeurs :
La démo est disponible ici :http://www.spacegoo.com/penrose